Projects
Optimal scheduling of refinery operations
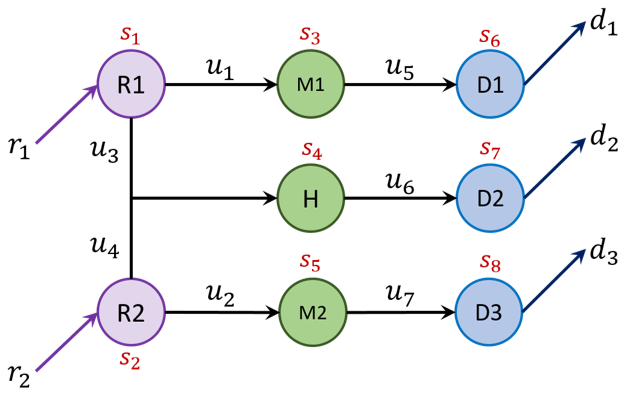Process scheduling problems in industrial plants can often be modeled as mixed-integer nonlinear programs (MINLPs) with a large number of constraints. While meta-heuristics, such as the simulated annealing (SA) algorithm or the genetic algorithm (GA) have been extensively employed to obtain high-quality solutions to MINLPs, their capabilities are often limited by the large number of combinatorial constraints and the time required to obtain these solutions. In view of these limitations, we aim to develop a hierarchical approach that leverages the capabilities of the high-level Reinforcement Learning (RL) algorithms and the computational savings of the low-level MILPs for optimal process scheduling subjected to static and temporal constraints. Besides addressing the hard operational constraints, our framework also accommodates for soft constraints, such as generating schedules that are fairly contiguous and avoid frequent switching between different operational modes.
Optimal strategies for inventory replenishment
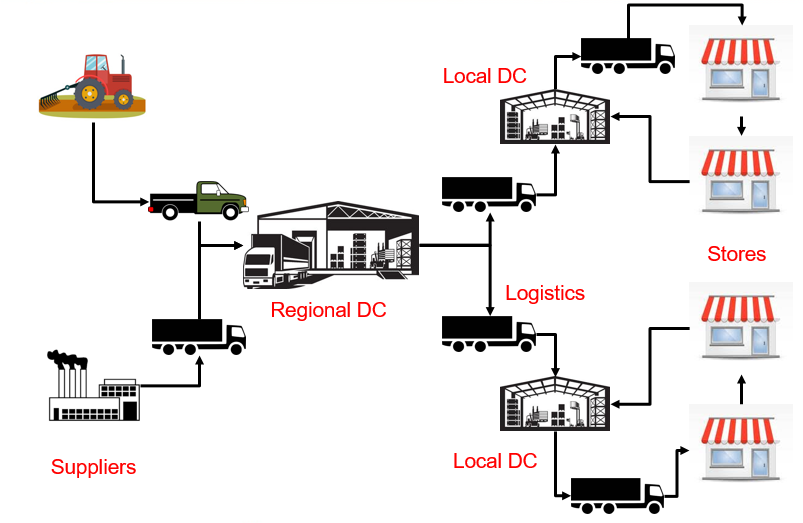Determining optimum inventory replenishment decisions is critical for retail businesses with uncertain demand. The problem becomes particularly challenging when multiple products with different lead times and cross-product constraints are considered. We address the aforementioned challenges in multi-product, multi-period inventory management using deep reinforcement learning. The proposed approach improves upon existing methods for inventory control on three fronts: (i) concurrent inventory management of a large number (hundreds) of products under realistic constraints, (ii) minimal retraining requirements on the RL agent under system changes through the definition of an individual product meta-model, (iii) efficient handling of multi-period constraints that stem from different lead times of different products. We approach the inventory problem as a special class of dynamical system control, and explain why the generic problem cannot be satisfactorily solved using classical optimization techniques. Subsequently, we formulate the problem in a general framework that can be used for parallelized decision-making using off-the-shelf RL algorithms. We also benchmark the formulation against the theoretical optimum achieved by linear programming under the assumptions that the demands are deterministic and known apriori. Experiments on scales between 100 and 220 products show that the proposed RL-based approaches perform better than the baseline heuristics, and quite close to the theoretical optimum. Furthermore, they are also able to transfer learning without retraining to inventory control problems involving different number of products.
Design of optimization algorithms
Accelerated gradient methods are the cornerstones of large-scale, data-driven optimization problems that arise naturally in machine learning and other fields concerning data analysis. We introduce a gradient-based optimization framework for achieving acceleration, based on the recently introduced notion of fixed-time stability of dynamical systems. The method presents itself as a generalization of simple gradient-based methods suitably scaled to achieve convergence to the optimizer in a fixed-time, independent of the initialization. We achieve this by first leveraging a continuous-time framework for designing fixed-time stable dynamical systems, and later providing a consistent discretization strategy, such that the equivalent discrete-time algorithm tracks the optimizer in a practically fixed number of iterations. We also provide a theoretical analysis of the convergence behavior of the proposed gradient flows, and their robustness to additive disturbances for a range of functions obeying strong convexity, strict convexity, and possibly non-convexity but satisfying the Polyak-Łojasiewicz inequality. We also show that the regret bound on the convergence rate is constant by virtue of the fixed-time convergence. The hyperparameters have intuitive interpretations and can be tuned to fit the requirements on the desired convergence rates. We validate the accelerated convergence properties of the proposed schemes on a range of numerical examples against the state-of-the-art optimization algorithms. Our work provides insights on developing novel optimization algorithms via discretization of continuous-time flows.
Learning to run power networks
Power grids transport electricity across states, countries and even continents. They are the backbone of world societies and economies, playing a pivotal economical and societal role by supplying reliable power to industry, and business and domestic consumers. Their importance appears even more critical today as we transition towards a more sustainable world within a carbon-free economy. Problems that arise within the power grid range from transient stability issues, localized blackouts to complete system or country-wide blackouts which can create significant economic and social perturbations . Grid operators are responsible for ensuring that a secure supply of electricity is provided everywhere, at all times, and that systems are designed to be both reliable and resilient. With the advent of renewable energy, electric mobility, and limitations placed on engaging in new grid infrastructure projects, the task of controlling existing grids is becoming increasingly difficult, forcing grid operators to do "more with less". We have developed RL-based solutions to address this important real-world problem for our future.
Tumor grading of histopathologic images
Early detection of Pancreatic Ductal Adenocarcinoma (PDAC), one of the most aggressive malignancies of the pancreas, is crucial to avoid metastatic spread to other body regions. Detection of pancreatic cancer is typically carried out by assessing the distribution and arrangement of tumor and immune cells in histology images. This is further complicated due to morphological similarities with chronic pancreatitis (CP), and the co-occurrence of precursor lesions in the same tissue. Most of the current automated methods for grading pancreatic cancers rely on extensive feature engineering involving accurate identification of cell features or utilising single number spatially informed indices for grading purposes. Moreover, sophisticated methods involving black-box approaches, such as neural networks, do not offer insights into the model’s ability to accurately identify the correct disease grade. We develop a novel cell-graph based Cell-Graph Attention (CGAT) network for the precise classification of pancreatic cancer and its precursors from multiplexed immunofluorescence histology images into the six different types of pancreatic diseases. The issue of class imbalance is addressed through bootstrapping multiple CGAT-nets, while the self-attention mechanism facilitates visualization of cell-cell features that are likely responsible for the predictive capabilities of the model. It is also shown that the model significantly outperforms the decision tree classifiers built using spatially informed metric, such as the Morisita-Horn (MH) indices.
Molecular property predictions
Development of new methods for analysis of protein-protein interactions (PPIs) at molecular and nanometer scales gives insights into intracellular signaling pathways and will improve understanding of protein functions, as well as other nanoscale structures of biological and abiological origins. We harness novel machine learning approaches to enable the design of nanoparticles (NPs) to control microbiome communities. Using a unique approach based on physical models and experimental data on nanomaterial synthesis and biological experiments, the ML model classifies and quantifies the relationships between nanoparticle characteristics and antimicrobial responses, providing hypotheses on the mechanisms of interactions between NPs and microorganisms.
Reduction of chemical networks
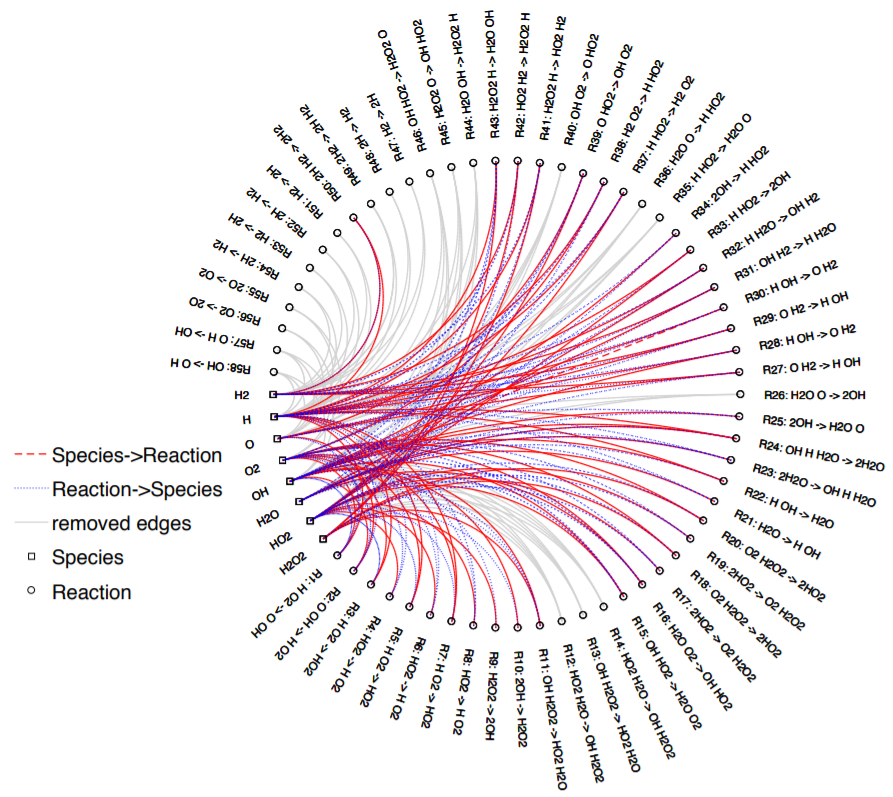Despite the increase in computational power over the last few decades, the modeling of complex reaction networks for realistic applications remains a daunting task. We have developed a data-driven sparse learning approach to model reduction in chemical reaction networks. Different from other methods presented in literature and studies, the proposed method does not require any understanding of the underlying process. Instead, it learns the model from data generated from the chemical process. And, the method requires tuning of only one parameter, the tolerance on the distance. Because of the data-driven nature of this approach, it can be implemented on any reaction mechanism. We have developed a general paradigm for network inference in the physical sciences and engineering with particular emphasis on dynamical chemical and biological reaction networks. Hybrid methods using machine learning (black-box) and mechanistic state space modeling (white-box) are of special interest.
Combinatorial Optimization Problems
Combinatorial optimization problems arise in many applications in various forms in seemingly unrelated areas such as data compression, pattern recognition, image segmentation, resource allocation, routing, and scheduling, graph aggregation, and graph partition problems. These optimization problems are characterized by a combinatorial number of configurations, where a cost value can be assigned to each configuration, and the goal is to find the configuration that minimizes the cost. Moreover, these optimization problems are largely non-convex, computationally complex and suffer from multiple local minima that riddle the cost surface. In our work, we are motivated by solutions that are employed by nature to similar combinatorial optimization problems; well described in terms of laws such as maximum entropy principle (MEP) in statistical physics literature. Our main current contributions are threefold - (i) First, we first provide a clustering or resource allocation viewpoint to several combinatorial optimization problems: (a) data clustering, (b) graph partitioning (such as clustering of power networks), (c) traveling salesman problem (TSP) and its variants, (d) vehicle routing problem with time-windows (VRPTW), (e) multiway cut, and (f) graph coloring. This viewpoint enables a unified approach to handle a broader class of problems, and therefore efficient MEP based heuristics can be leveraged to obtain high-quality solutions. (ii) Second, we explore MEP based ideas to clustering problems specified by pairwise distances. Many problems in graph theory are indeed specified in terms of the corresponding edge-weight matrices (and not in terms of the nodal locational coordinates). (iii) Finally, our framework allows for inclusion of several constraints in the clustering/resource allocation problems. These constraints may correspond to capacity constraints in case of resource allocations where capacity of each resource is limited, or minimum-tour length constraints in case of traveling salesman problems (TSPs) and its variants.
Enabling the Grid of the Future
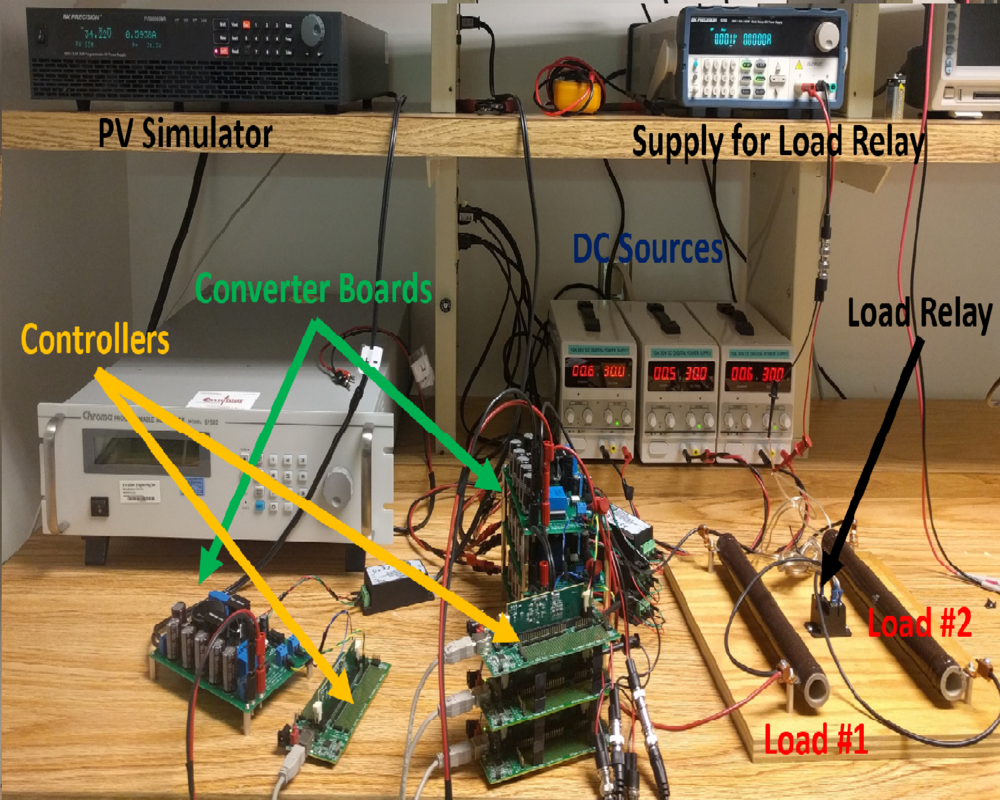The infrastructure that defines the U.S. electric grid is based largely on pre-digital technologies developed in the first part of the 20th century. In subsequent decades, grid development has evolved through emphasis on safety, accessibility, and reliability to security and resiliency. Throughout this evolution, the grid mainly relied on centralized power plants and developed protocols to provide system reliability based on that model. However, the increasing use of renewable generation and distributed energy resources (DER), such as residential solar and home energy storage, along with customers’ changing energy usage patterns are leading to greater uncertainty and variability in the electric grid. New tools are required to create a flexible and modern electric grid that can meet this increase in renewable generation and DERs, while providing the quality of service, resiliency, and reliability that customers expect. We have developed innovative hardware and software solutions to integrate and coordinate generation, transmission, and end-use energy systems at various points on the electric grid. These control systems will enable real-time coordination between distributed generation, such as rooftop and community solar assets and bulk power generation, while proactively shaping electric load.